Could you tell us a bit about yourself?
My name is Philipp Seiler. I studied Mechanical Engineering and Mechatronics in my undergrad in Germany, at the TU Braunschweig. I did my PhD in a completely different topic, in Material Science. After that, I went to the US, where I went to Purdue University to do a post-doc, then to the UK where I was a research associate at the University of Cambridge for 6 years. After that, I became a lecturer (assistant professor) at the University of Kent. I transferred very recently to Canada.
In my research, I work on materials under extreme conditions – for example, materials for rocket engines or gas turbines. I would like to answer questions like how we can design systems that can withstand very high temperatures. The other part of my research is about lightweight materials: how can you make these material structures light weight, but still make them very strong, stiff, and tough. For that, linear algebra is very important.

“I don’t think there is a single day where I don’t use linear algebra.”
There are many tools, such as Finite Element Analysis (FEA), a tool that can predict stresses and strains that use linear algebra. This tool basically solves a system of differential equations. But instead of solving two or three equations, you’re looking at a system of millions of equations. So, it’s very important to know the underlying physics as well as the algorithms used, to understand and interpret the results.
Could you describe your teaching style and your favorite part of teaching?
Teaching is an integral part of being a professor. I like interacting with students, and I really enjoy seeing students grasp complex concepts during a lecture. It is amazing to meet former students a few years later and see them on track to get into their dream career.
I have an active teaching style, even with a large cohort size.
“I like going on academic detours – I would change the lectures when I see what students are interested in a certain topic.”
I do not plan lectures down to the minute. I come to lectures with a brief outline, then I see how the students follow and react. In particular, teaching linear algebra is like teaching a programming language. I start with the basic “commands,” such as vector spaces, vectors, matrices, etc., and then I apply these tools to solve equations in real world problems.
Why do engineers need to learn proofs, and do you have any tips for mastering them?
If I were to simply teach how a tool like matrix multiplication works, e.g. just by following an algorithm, students would quickly forget it. By knowing the proofs, you can understand why and how matrix operations work. Even if you forget the details, it will be easier to relearn it. Moreover, proofs can help students understand linear algebra conceptually.
“I want students to understand why certain concepts are true and why they work.”
Reading the textbook over the whole term is very important, so don’t just start before any midterm or exam. Also, continuously put work and effort into learning and following the lectures. While the learning curve isn’t steep in the beginning, it picks up very quickly, so you have to be on top of things. If you have questions, come to office hours or ask me after the lectures. I hope students are engaged and ask as many questions as possible.
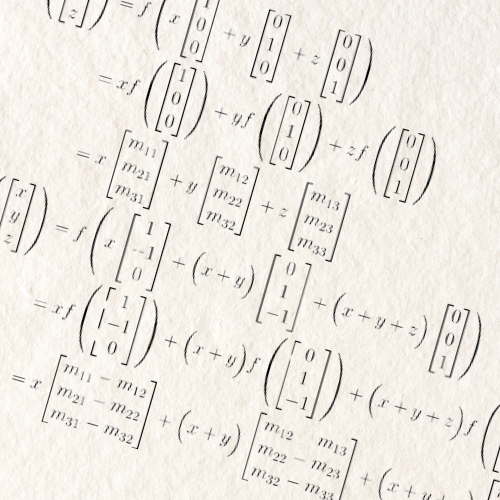
What can students expect from this course, and what is the key takeaway you want them to learn?
“I would like students to forget what they learned in high school”.
One by one, I will introduce the necessary concepts for them to understand what matrices are. Lectures are typically based on proofs, where I introduce a tool and explain why it works. Lectures are in general more theoretical, but there are plenty of opportunities to get examples, exercises, and additional material.
[In terms of takeaways, ] they should know the fundamentals – what a matrix is, what a vector is, what are vector spaces, and how to use them. If I teach you the concept, that way you can learn to use it and apply it to different applications.
How does linear algebra connect with your work, research, or engineering in general?
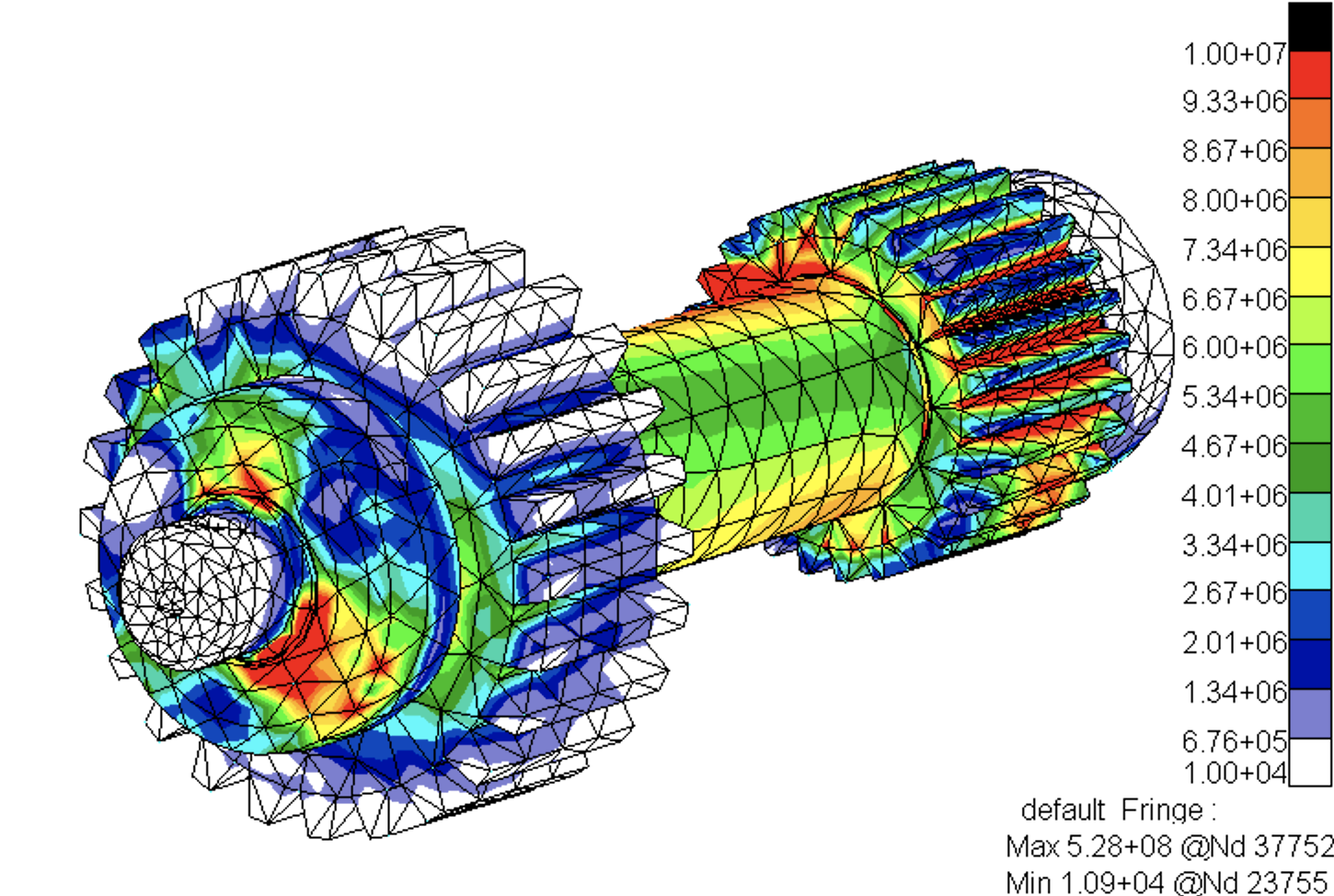
Novel methods of artificial intelligence are typically highly non-linear. The question becomes, why is linear algebra still important? Linearizing a system of equations is still very powerful.
“Even machine learning technologies are all based on linear algebra.”
As I mentioned earlier, I’m doing research in materials science. If you are designing structures or materials, you are typically interested in predicting stresses and strains. One tool we use for these predictions is FEA and this is nothing but solving matrix equations. Here you could have a million-by-million matrix. Methods of linear algebra are used to efficiently solve these systems of equations. Nowadays, I don’t solve these systems by hand, but I should know how the results will look like and be able to interpret them. FEA produces colorful pictures, but just because they are colorful doesn’t mean they are true. You need to understand how stresses are computed and how the numerical solver works.
A second application of linear algebra is robotics. Let’s say you want to model a robotic arm by direct kinematics. Again, you are using matrix operations to describe the robotic system. For example, each joint of the robotic arm can be described as a matrix, representing translation and rotation. By using a matrix multiplication of the matrices of each joint, we can calculate the behaviour of the whole robotic arm.
Any other comments or thoughts to share?
For this course, ChatGPT is not a very useful tool to understand the proofs in the textbook. Currently, problems solved with ChatGPT can be false while still looking plausible.
